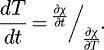EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 116 / No 6 (2019) Metall. Res. Technol., 116 6 (2019) 615 Full HTML
Open Access
Issue
Metall. Res. Technol.
Volume 116, Number 6, 2019
Article Number 615
Number of page(s) 5
DOI https://doi.org/10.1051/metal/2019037
Published online 17 September 2019

© O. Bouaziz, published by EDP Sciences, 2019

Licence Creative Commons
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

In the field of solid-state phase transformation in metallic alloys [1], the transformation of austenite in steel on cooling can occur by a variety of mechanisms including the formation of ferrite, bainite and martensite. The bainitic transformation occurs in a range between purely diffusional transformation to ferrite or pearlite and low temperature transformation to martensite by a displacive mechanism. Thus, the bainite transformation exhibits features of both diffusional and displacive transformations and has given rise to a large amount of research activity (see [2,3] for reviews). A major part of the research has concerned modelling of the kinetics of the transformations by detailed descriptions of the thermodynamic conditions operating at the interface [4–7]. However, the crucial understanding of the physically based conditions of the start of each phase transformation is less understood, especially for bainite.

Usually the Ar3 temperature is defined as the maximum temperature for any phase transformation of austenite to ferrite during cooling [8]: 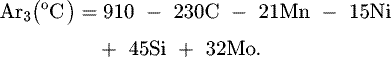(1)

For temperature lower than Ar3, the basical tools of physical metallurgy are the definition of the martensite start temperature Ms and the bainite start temperature Bs expressed phenomenologically as functions of chemical composition as: 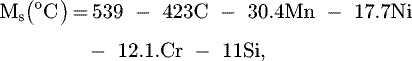(2) where alloying element are expressed in weight(%) [9], and [10]: 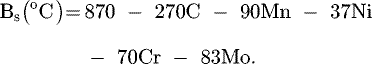(3)

In addition, another characteristic temperature is defined as the temperature where austenite and ferrite has the same thermo-chemical free energy determined as [2,11]: 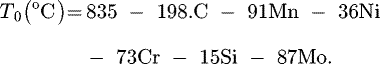(4)

In this publication, it is showed that it is possible to describe in a global approach the conditions for each phase transformation exploiting completely Landau’s theory [12–15] of phase transformations including an original order parameter and to propose a new classification of the different phase transformation in steel during cooling and to predict naturally the effect of cooling rate on bainite start temperature.

2 The proposed approach

In the framework of Landau’s theory [12–14], for a second order phase transition, the free energy is expressed as: (5) where T is the temperature, χ the order parameter, F0(T) the thermo-chemical free energy, A(T) a function of temperature and C a positive constant.

The simplest expression for A(T) is: 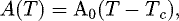(6) with A0 a positive constant and Tc a critical temperature where A(T) changes of sign.

Usually in phase transformation of steels, F0(T) is known [2,3,7]. So, the identification of the total free energy F (χ, T) requires the determination of three parameters: A0, Tc, C.

For T > Tc, F (χ, T) exhibits one minimum as a function of χ: 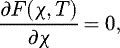(7) for χ = 0

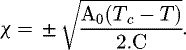For T ≤ Tc, F (χ, T) exhibits two minima as a function of χ: (8) for (9)

In order to exploit this approach to a classification of phase transformations in steel, it is now assumed that: 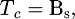(10) where Bs is the bainite start temperature.

By convention, it is chosen to have an order parameter for martensite: 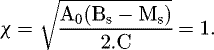(11)

Giving a first relationship: 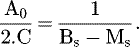(12)

Therefore, the order parameter is: 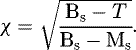(13)

As Bs to Ms temperatures depends on the carbon content, this one controls the order parameter.

In order to illustrate quantitatively this law, the evolution of the order parameter from Bs to Ms temperatures for two different Fe–C compositions has been plotted in Figure 1.

It is now proposed to define clearly what could be the parameter of order for phase transformation in steels. If Cf is the carbon content of the phase appearing, it is reasonable to propose that: 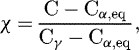(14) Where 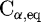is the solubility of carbon in ferrite at equilibrium and 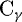is the carbon in austenite. So, the order parameter can be a sursaturation in carbon in the binary Fe–C system.

In addition, chemical free energy at Ms has been determined as [14]: 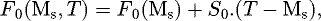(15) with F0(Ms) = 1250 J/mol and S0 = −6.8 J.mol−1.K−1, which are independent of the composition.

The energy value F0(Ms) should correspond to the maximum at Ms for χ = 0. As for any T < Bs this maximum exists for the same value of χ = 0, it is written for 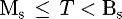: 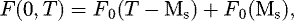(16) with 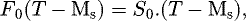(17)when T is near Ms but it can be completely different for higher temperature.

In order to determine A0 and C, as the total free energy at Ms for χ = 1 has to be zero, it comes: 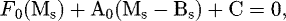(18) or (19)and 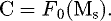(20)Consequently: 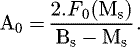(21)

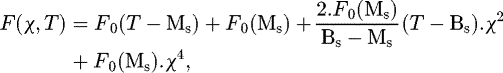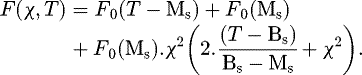Finally it is possible to express completely the free energy: (22) or (23)

In order to highlight the key role of the order parameter, it has been drawn in Figure 2. The evolution of the right-end side term of the expression: 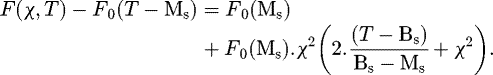(24)

Finally, the quantitative developed approach can be used in order to summarized the thermodynamic conditions for the formation of each phase, as it is summarized in Table 1, providing more rigorous occurrence criterion especially to distinguish ferrite, bainite or martensite formation.

thumbnail Fig. 1

Evolution of the order parameter from Bs to Ms temperatures for two different Fe–C compositions.
thumbnail Fig. 2

Evolution of the as a function of the order parameter at Bs and at Ms temperatures.
Table 1

Classification of phase transformation conditions from austenite during cooling.

3 Extended approach including cooling rate

It is well known that Bs decreases if the cooling rate is increased. In order to capture this effect using the previous approach, it is assumed that a kinetic equation for the order parameter can be written for T < Bs as: 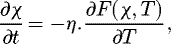(25) where η is independent of χ and of T, giving for T < Bs: 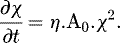(26)

Using equation (13), it is also possible to express: 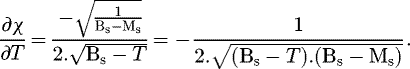(28)

Therefore: (27)

It comes using equations (26) and (28): 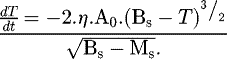(30)

Combining with equation (21), we have: 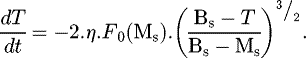(32)

Thus, the temperature T respecting equation (32) is: 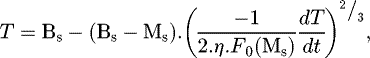(33) with during cooling. This temperature is the bainite start temperature affected by the cooling rate.

As , equation (33) gives a critical cooling rate for T = Ms: (34)

In addition, a formula has been determined for the critical cooling rate in order to form 1% of martensite from austenite [16]: 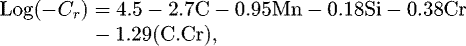(35) where Cr is expressed in °C/s.

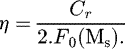Moreover, using equation (34) and (35), it is consistent to impose that: (36) and (37)

Finally, the law predicting the evolution of the bainite start temperature as a function of cooling rate is: (38)

In order to illustrate quantitatively this law, the evolution of the bainite start temperature as a function of cooling rate for two different Fe–C compositions has been plotted in Figure 3.

thumbnail Fig. 3

Evolution of the bainite start temperature as a function of cooling rate for two different Fe–C compositions.

4 Conclusions

Exploiting Landau’s theory of phase transformations, defining an original order parameter and using the phenomenological transformation temperatures, it is reported that it is possible to describe in a global approach the conditions for the formation of each phase (ferrite, bainite, martensite) from austenite during cooling in steel. It allowed to propose a new rigorous classification of the different thermodynamic conditions controlling each phase transformation. In a second step, the approach predicts naturally the effect of cooling rate on the bainite start temperature. In perspectives, the approach can be extended to take into account external fields by adding a linear term in free energy linearly proportional to the order of parameter and proportional to the potential energy of the external field [12–14]. For instance, in the case of an uniaxial applied stress σ, the contribution to the free energy is expressed as: 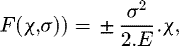(39) where E is the elastic modulus and the sign depends on the compressive or tensile stress.

This term breaks the symmetry of the total free energy as a function of the parameter of order and it can change the occurrence conditions of each phase. A lot of experimental data are available is the literature in order to validate this last point which will be investigated in a next future.

Acknowledgement

The author thanks Dr. F. Levy for stimulating discussions.

References

  1. M. Hillert, Phase equilibria, Phase diagrams and Phase tranformations, 2nd ed., Cambridge University Press, Cambridge, UK, 2008 [Google Scholar]
  2. H.K.D.H. Bhadeshia, Bainiet in steels, 2nd ed., IOM Communication Ltd., London, 2001 [Google Scholar]
  3. M. Hillert, Paraequilibrium and other restricted equilibria, in: L.H. Bennet, T.B. Massalski, B.C. Giessen (Eds), Alloy phase diagrams, Mater. Res. Soc. Symp. Proc. 19, 295 (1983). [Google Scholar]
  4. J.S. Kirkaldy, Can. J. Phys. 36, 907 (1958) [Google Scholar]
  5. A. Hultgren, Trans. ASM. 39, 915 (1947) [Google Scholar]
  6. M. Takahashi, Curr. Opin. Solid State Mater. Sci. 8, 213 (2004) [Google Scholar]
  7. H.S. Zurob, C.R. Hutchinson, Y. Bréchet, H. Seyedrezai, G. Purdy, Acta Mater. 57, 2781 (2009) [Google Scholar]
  8. F.B. Pickering, Steels: Metallurgical principles, in: Encyclopedia of Materials Science and Engineering, Vol. 6, The MIT Press, Cambridge, 1986 [Google Scholar]
  9. K.W. Andrews, J. Iron Steel Inst. 203, 721 (1965) [Google Scholar]
  10. W. Steven, A.G. Haynes, JISI. 183, 349 (1956) [Google Scholar]
  11. S.M.C. Van Bohemen, Metall. Trans. A 41, 285 (2010) [CrossRef] [Google Scholar]
  12. L.D. Landau, E.M. Lipschitz, Statistical Physics, Pergamon, London, 1959 [Google Scholar]
  13. R.A. Cowley, Adv. Phys. 29, 1 (1980) [Google Scholar]
  14. F. Falk, J. Phys. Colloq. 43, C-4-3 (1982) [Google Scholar]
  15. J. Wang, S. Van der Zwaag, Metall. Trans. A 32, 1527 (2001) [CrossRef] [Google Scholar]
  16. A. Moulin, ArcelorMittal Research, Internal Report, 2001 [Google Scholar]

Cite this article as: Olivier Bouaziz, An original unified approach for the description of phase transformations in steel during cooling: first application to binary Fe–C, Metall. Res. Technol. 116, 615 (2019)

All Tables

Table 1

Classification of phase transformation conditions from austenite during cooling.

In the text

All Figures

thumbnail Fig. 1

Evolution of the order parameter from Bs to Ms temperatures for two different Fe–C compositions.
In the text
thumbnail Fig. 2

Evolution of the as a function of the order parameter at Bs and at Ms temperatures.
In the text
thumbnail Fig. 3

Evolution of the bainite start temperature as a function of cooling rate for two different Fe–C compositions.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.