| Issue |
Metall. Res. Technol.
Volume 119, Number 4, 2022
|
|
|---|---|---|
| Article Number | 419 | |
| Number of page(s) | 4 | |
| DOI | https://doi.org/10.1051/metal/2022064 | |
| Published online | 11 July 2022 | |
Regular Article
Assessment of a physical based modelling suitable to capture the mechanical behaviour at large plastic strain of aluminium alloys
1
Laboratoire d’Etude des Microstructures et de Mécanique des Matériaux (LEM3), CNRS, Université de Lorraine, Arts et Métier Paris Tech, 57000 Metz, France
2
LABoratoire d’EXcellence DAMAS, Université de Lorraine, 57000 Metz, France
3
106 Nicholson Point, Ontario, KOH 1GO, Canada
* e-mail: olivier.bouaziz@univ-lorraine.fr
Received:
23
March
2022
Accepted:
24
June
2022
It is reported for the first time the application of a physical-based constitutive law suitable to capture the flow stress and the strain-hardening in a wide range of plastic strain. This law is validated by comparison with experiments related to alloying elements effect and temperature in aluminium alloys especially characterized by bulge test at room and at warm temperature.
Key words: stress / strain / bulge test / modelling
© O. Bouaziz and D. Lloyd, Published by EDP Sciences, 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Tensile tests usually characterize the mechanical behaviour of materials. This test is limited due to necking occurrence at quite small strain lower than 30%. Unfortunately, there is a strong demand for behaviour laws to describe the behaviour for strains beyond the necking strain, especially for forming operations such as deep-drawing, roll forming, or rolling to predict force etc.
Bulge test set-up as illustrated in Figure 1a, is well known to be suitable for a mechanical characterization beyond the uniaxial tensile strain at necking [1,2]. In bulge test, if the material is assumed isotropic and if the deformation is assumed to be a spherical cap, it comes from Figure 1b [1,2].
The radius of curvature is:
 (1)
(1)
The maximum equivalent strain is:
 (2)
(2)
And the maximum Von Mises equivalent stress is given as:
 (3)
(3)
Different round robins are available in the literature [3–8] comparing the prediction of mainly Hollomon [8], Swift [9], and Voce [10] laws respectively expressed as:
 (4)
(4)
 (5)
(5)
 (6)where σ and ε are respectively the Von-Mises equivalent stress and the Von-Mises equivalent plastic strain. The others parameters are fitting constants.
(6)where σ and ε are respectively the Von-Mises equivalent stress and the Von-Mises equivalent plastic strain. The others parameters are fitting constants.
We can notice that Kocks-Mecking has obtained the Voce law by physical arguments [11]. In this publication, the Voce law is now referred to as KM.
It has been concluded that none of these laws are suitable to capture the evolution of flow stress as a function of strain in a wide range of plastic strains. On the contrary, a new physical based behaviour law has been recently proposed [12] and is given by:
 (7)
(7)
seems to be promising for this issue where σo, θo, and σs are three parameters to be identified. θo controls the initial work-hardening (stage 2) and σs controls the saturation of the stress-strain relationship.
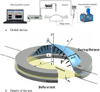 |
Fig. 1 Principle of bulge test. |
2 Experiments and modelling
At first, the new approach has been compared to K-M law concerning the evolution of flow stress in plane stress [12]. It is highlighted in [12] that the two approaches give similar results for low flow stress, but the new one avoids a rapid saturation of strain-hardening for higher stresses which is more consistent with all the available experimental data.
In order to go further, experimental data related to the alloying element (Magnesium) have been selected, especially because they are available in a wide range of plastic strain because obtained by bulge-test used in pioneering work developed in Alcan Research Center [13]. The presented data have already been showed in oral presentation about twenty years ago but they have never been published. All the aluminium alloys have been cast, rolled and heat-treated and quenched Alcan Research Center in order to have the elements in solid solution. Figure 2 shows the agreement between experiments and modelling whatever the plastic strain. The identification of the parameters is reported in Table 1 and plotted in Figure 3. The results highlight that the solute content increases the strain-hardening in stage 2 before saturation, and it regularly increases the stress σs.
As shown in Figure 4, the temperature exhibits a strong effect on flow stress during a bulge test. The proposed approach is suitable to capture this effect with a constant value of strain-hardening in stage 2 but with an increase in the critical stress σs, i.e. the dynamic recovery as reported in Table 2.
 |
Fig. 2 Comparison between experimental and predicted stress-strain curves in bulge test for different Al-Mg alloys. |
Identified values of the parameters of the modelling as a function of solute content.
 |
Fig. 3 Evolution of the parameters as a function of magnesium content (dots for θo and diamonds for σs). |
 |
Fig. 4 Assessment of the modelling as a function of temperature for Al-0.2%Cu alloy during a bulge test. |
Identified values of the parameters of the modelling as a function of the temperature.
3 Conclusions
A physical behaviour law has been assessed with a very limited number of constants. For the first time, this law has been validated in a wide range of plastic strains considering solutes and temperature in aluminium alloys using data provided by bulge test.
The avenues are numerous:
Prediction of Yield Stress, Ultimate Tensile Strength and Uniform Elongation in tension.
Application of this law to other metallic materials.
Easy implementation in Finite Element Code for forming simulations.
Include the strain rate effect.
Competing interests
The authors declare that they have no conflict of interest.
References
- K. Lange, Handbook of metal forming, McGraw-Hill, New York (1985) [Google Scholar]
- T. Altan, H. Palaniswamy, P. Bortot et al., Determination of sheet material properties using biaxial tests, in Proceedings of the 2nd International Conference on Accuracy in Forming Technology, Chemnitz, Germany (2006) [Google Scholar]
- M.K. Gupta, N.M. Singh, Modelling and simulation on deformation behaviour of Al2014-T6 alloy beyond necking, Mater. Today: Proc. 44, 4204–4208 (2021) [CrossRef] [Google Scholar]
- J. Cao, F. Li, X. Ma et al., Tensile stress−strain behavior of metallic alloys, Trans. Nonferrous Met. Soc. China 27, 2443–2453 (2017) [CrossRef] [Google Scholar]
- S.K. Kang, Y.C. Kim, K.H. Kim et al., Constitutive equations optimized for determining strengths of metallic alloys, Mech. Mater. 73, 51–57 (2014) [CrossRef] [Google Scholar]
- W.M. Sing, K.P. Rao, Role of strain-hardening laws in the prediction of forming limit curves, J. Mater. Process. Technol. 63, 105–110 (1997) [CrossRef] [Google Scholar]
- H. Yang, H. Li, J. Ma et al., Constitutive modeling related uncertainties: effects on deformation prediction accuracy of sheet metallic materials, Int. J. Mech. Sci. 157–158, 574–598 (2019) [CrossRef] [Google Scholar]
- J.H. Hollomon, Tensile deformation, AIME Trans. 124, 1–22 (1945) [Google Scholar]
- H.W. Swift, Plastic instability under plane stress, J. Mech. Phys. Solids 1, 1–18 (1952) [CrossRef] [Google Scholar]
- E. Voce, The relationship between stress and strain for homogeneous deformation, J. Inst. Met. 74, 537–562 (1948) [Google Scholar]
- H. Mecking, U.F. Kocks, Physics and phenomenology of strain hardening, the FCC case, Prog. Mater. Sci. 48, 171–273 (2003) [CrossRef] [Google Scholar]
- O. Bouaziz, Revisited storage and dynamic recovery of dislocation density evolution law: toward a generalized Kocks-Mecking model of strain-hardening, Adv. Eng. Mat. 1–3 (2012) [Google Scholar]
- D.J. Lloyd, H. Sang, J.D. Embury et al., On the description of deformation at large imposed plastic strains, Mater. Sci. Eng. 36, 35–46 (1978) [CrossRef] [Google Scholar]
Cite this article as: Olivier Bouaziz, David Lloyd, Assessment of a physical based modelling suitable to capture the mechanical behaviour at large plastic strain of aluminium alloys, Metall. Res. Technol. 119, 419 (2022)
All Tables
Identified values of the parameters of the modelling as a function of solute content.
Identified values of the parameters of the modelling as a function of the temperature.
All Figures
 |
Fig. 1 Principle of bulge test. |
| In the text | |
 |
Fig. 2 Comparison between experimental and predicted stress-strain curves in bulge test for different Al-Mg alloys. |
| In the text | |
 |
Fig. 3 Evolution of the parameters as a function of magnesium content (dots for θo and diamonds for σs). |
| In the text | |
 |
Fig. 4 Assessment of the modelling as a function of temperature for Al-0.2%Cu alloy during a bulge test. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


